Selon une rumeur assez répandue, il arrivait souvent que les propriétaires d’une célèbre voiture – produite par un grand constructeur automobile italien dans les années 80, et particulièrement répandue en blanc – ouvrent par erreur, avec leur propre clé, la voiture de quelqu’un d’autre, la prenant pour la leur dans un parking, à la sortie du cinéma ou d’un concert.
Il ne s’agit peut-être que d’une légende urbaine, mais elle nous fait réfléchir à un aspect important pour la sécurité : combien y a-t-il de clés différentes pour une serrure donnée ? En d’autres termes, quelle est la probabilité qu’une personne en possession d’une clé puisse ouvrir une autre serrure du même type, en plus de la sienne ? Ce n’est pas une simple curiosité. Il y a des situations où cela peut réellement se produire. Dans une grande copropriété, par exemple, où il y a des dizaines de boîtes aux lettres avec la même serrure, une seule clé peut-elle en ouvrir deux ?Faisons quelques calculs. Le nombre de clés théoriquement possibles pour un cadenas, un cylindre ou une serrure à goupilles dépend du nombre de chiffrages possibles pour la serrure en question, c’est-à-dire du nombre de combinaisons possibles entre les hauteurs des goupilles insérées dans le barillet ; les combinaisons se calculent en prenant le nombre des hauteurs possibles des goupilles et en l’élevant au nombre de goupilles elles-mêmes.

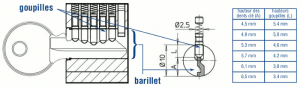Pour cette raison, des usinages plus précis permettent de réaliser des serrures plus sûres car ils permettent d’insérer, dans un barillet donné, un plus grand nombre de goupilles et d’obtenir de chaque piston – à égalité de longueur – plusieurs hauteurs utiles. Cela se traduit par une augmentation significative du nombre de combinaisons possibles. Par exemple : une serrure avec 3 goupilles de 4 hauteurs chacune pourrait avoir seulement 4³=64 combinaisons théoriques. Si, avec des usinages plus précis, on arrive à obtenir 5 hauteurs au lieu de 4, les combinaisons deviennent 5³=125. Si on arrive encore à insérer 4 goupilles au lieu de 3, on obtient 625 (5⁴) combinaisons, et ainsi de suite.
Il faut aussi tenir compte du fait que certains chiffrages doivent être éliminés du nombre des chiffrages théoriquement possibles. Au départ, on doit éliminer tous les chiffrages dans lesquels toutes les goupilles ont la même hauteur. Ceux-ci ne sont évidemment pas sûrs car la serrure pourrait être ouverte avec n’importe quelle lame ou tige de fer utilisée pour abaisser simultanément toutes les goupilles. Deuxièmement, on doit éliminer les chiffrages qui ont une alternance trop brusque entre les hauteurs maximales et minimales des goupilles et qui peuvent donc rendre difficile l’introduction et/ou l’extraction de la clé. Dans les serrures de mauvaise qualité, ces combinaisons ne sont presque jamais éliminées, alors que la nécessité de les éliminer rend encore plus essentielle l’obtention d’un nombre élevé de chiffrages théoriquement possibles étant donné que le nombre réellement utilisable est ensuite inférieur. En prenant l’exemple le plus simple, celui de la serrure avec 3 goupilles et 4 hauteurs, on a 4 combinaisons avec les goupilles à la même hauteur ; en les éliminant, on a 60 combinaisons possibles, et 14 combinaisons où une hauteur maximum et une hauteur minimum sont consécutives ; en les éliminant elles aussi, on a seulement 46 combinaisons réellement utilisables. Si dans une copropriété comptant plus de 46 appartements on utilise une serrure de ce type pour les boîtes aux lettres, il est statistiquement certain qu’il y a au moins un copropriétaire qui peut lire le courrier de quelqu’un d’autre…
Et vous, avez-vous déjà ouvert une autre serrure avec votre clé ?
Regardez comment on assemble une serrure
Regardez le catalogue des produits Viro